What are some metrics for Named Entity Recognition?
Contents
What are some metrics for Named Entity Recognition?#
Contributor(s): Lee Xin Jie, Senior AI Engineer (100E)
Named Entity Recognition#
Named Entity Recognition refers to the task for locating and classifying named entities in text documents.
This article assumes prior knowledge of the IOB (also known as BIO) format for entity tagging. IOB stands for inside, outside and beginning, where outside (O) indicates a token not belonging to an entity, beginning (B) indicates a token is the start of an entity and inside (I) indicates a token is inside an entity. You may refer to this article for more information on the IOB format.
NER can be thought of as a token level classification problem. Hence, NER models are often tuned using metrics such as F1, precision, recall at a token level during model training. When it comes to evaluating NER models on their downstream tasks’ performance, it may be more beneficial to aggregate the individual tokens into full named-entities, and evaluate NER models at a full named-entity level against golden standard annotations. This also makes the evaluation more relatable for the client.
There are multiple evaluation schemes for evaluating NER models at a full named-entity level. This article will focus on the SemEval (International Workshop on Semantic Evaluation) scheme, which is one of the most popular schemes. The SemEval scheme is built off the Message Understanding Conferene (MUC) scheme.
Before we dive deeper into the SemEval scheme, ley us take a brief look into the MUC scheme. The MUC scheme introduces 5 categories to reflect the correctness of the full named-entities, and the classes are as follows. For a further read up on the MUC scheme, refer to this link
Evaluation Scheme |
Explanation |
|---|---|
Correct (COR) |
The output of a system and the golden annotation are the same |
Incorrect (INC) |
The output of a system and the golden annotation don’t match |
Partial (PAR) |
System and the golden annotation are somewhat “similar” but not the same |
Missing (MIS) |
A golden annotation is not captured by a system |
Spurius (SPU) |
System produces a response which doesn’t exist in the golden annotation |
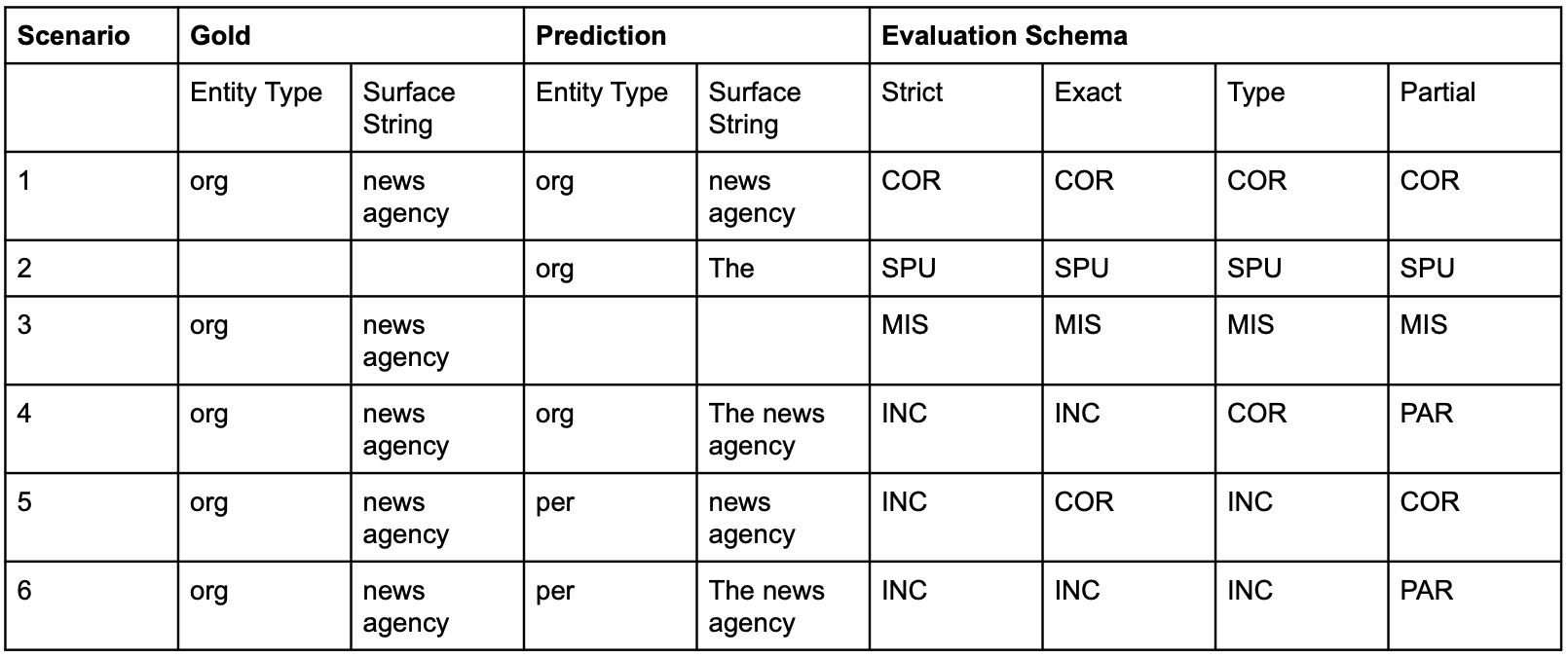
In the SemEval scheme, there are 4 options of measuring the overall performance. They differ in terms of what is considered to be correct, incorrect, partial, missed and spurious predictions. Specifically, these 4 options indicate the correctness of the full named-entities with respect to their boundaries and entity classes. All 4 options can be applied to the computation of F1, precision and recall. A detailed explanation can be found in this blog.
Evaluation Scheme |
Explanation |
|---|---|
Strict |
Exact boundary surface string and entity type |
Exact |
Exact boundary match over the surface string, regardless of the type |
Partial |
Partial boundary match over the surface string, regardless of the type |
Type |
Some overlap between the system tagged entity and the gold annotation is required |
To illustrate the SemEval scheme with an example, consider the same example as before.
Token |
Gold Labels |
|---|---|
The |
Other |
news |
Org |
agency |
Org |
is |
Other |
here |
Other |
Next, we compute the total number of gold annotations with the formula:
\(Possible (POS) = COR + INC + PAR + MIS = TP + FN\)
The total annotations produced by the system is:
\(ACTUAL (ACT) = COR + INC + PAR + SPU = TP + FP\)
To compute the precision and recall for Strict and Exact:
\(Precision = \frac{COR}{ACT} = \frac{TP}{TP + FP}\)
\(Recall = \frac{COR}{POS} = \frac{TP}{TP + FN}\)
To compute the precision and recall for Partial and Type:
\(Precision = \frac{COR + 0.5 \times PAR}{ACT} = \frac{TP}{TP + FP}\)
\(Recall = \frac{COR + 0.5 \times PAR}{POS} = \frac{COR}{ACT} = \frac{TP}{TP + FP}\)
To compute the F1, precision and recall for the example above:
Measure |
Partial |
Type |
Exact |
Strict |
|---|---|---|---|---|
Correct |
2 |
2 |
2 |
1 |
Incorrect |
0 |
2 |
2 |
3 |
Partial |
2 |
0 |
0 |
0 |
Missed |
1 |
1 |
1 |
1 |
Spurius |
1 |
1 |
1 |
1 |
Precision |
0.6 (a1) |
0.4 (b1) |
0.4 (c1) |
0.2 (d1) |
Recall |
0.6 (2) |
0.4 (b2) |
0.4 (c2) |
0.2 (d2) |
F1 |
0.6 |
0.4 |
0.4 |
0.2 |
Reference for calculation:
a1) \(\frac{2 + 0.5 \times 2}{2 + 0 + 2 + 1} = \frac{3}{5}\)
a2) \(\frac{2 + 0.5 \times 2}{2 + 0 + 2 + 1} = \frac{3}{5}\)
b1) \(\frac{2 + 0.5 \times 0}{2 + 2 + 0 + 1} = \frac{2}{5}\)
b2) \(\frac{2 + 0.5 \times 0}{2 + 2 + 0 + 1} = \frac{2}{5}\)
c1) \(\frac{2}{2 + 2 + 0 + 1} = \frac{2}{5}\)
c2) \(\frac{2}{2 + 2 + 0 + 1} = \frac{2}{5}\)
d1) \(\frac{1}{1 + 3 + 0 + 1} = \frac{1}{5}\)
d2) \(\frac{1}{1 + 3 + 0 + 1} = \frac{1}{5}\)
In general, partial will be the most lenient evaluation, while strict will be the most stringent evaluation. The scores for type and exact will usually fall in between partial and strict.
If getting both the boundaries and the classes of the full named-entities are important, then strict will be the measure that you should prioritise. If it is only critical to get the boundaries correct, then exact will be the more appropriate measure to optimise for. Likewise, if it is only critical to get the classes correct and it is acceptable to get partial boundary overlaps, then type will be the more appropriate measure. Lastly, if only partial boundary overlaps are required and it is not important to get the classes correct, then partial can be the preferred measure. Generally, it is more common for type and exact to be preferred. You should check what the client’s requirements are before making a decision as to which to prioritise.
 Horizontal Logo CMYK Full Colour.png)